Research
My work is highly interdisciplinary and love learning new areas to apply mathematics to explain natural phenomena, so please reach out if you are interested in collaborating or general discussion!
Partial Differential Equation and Fluid-Structure Interaction
Bioconvection
Bioconvection refers to the patterns formed by the interaction between a viscous fluid and vertically swimming micro-organisms under the influence of gravity. These micro-organisms, typically oblong with the center of mass near the tail, swim toward the fluid surface, accumulating at the top until a critical population density is reached. This creates an instability that pulls the concentrated cells to the bottom, forming dynamic patterns sensitive to variations in cell shape, fluid viscosity, and domain geometry and observed both experimentally and computationally.
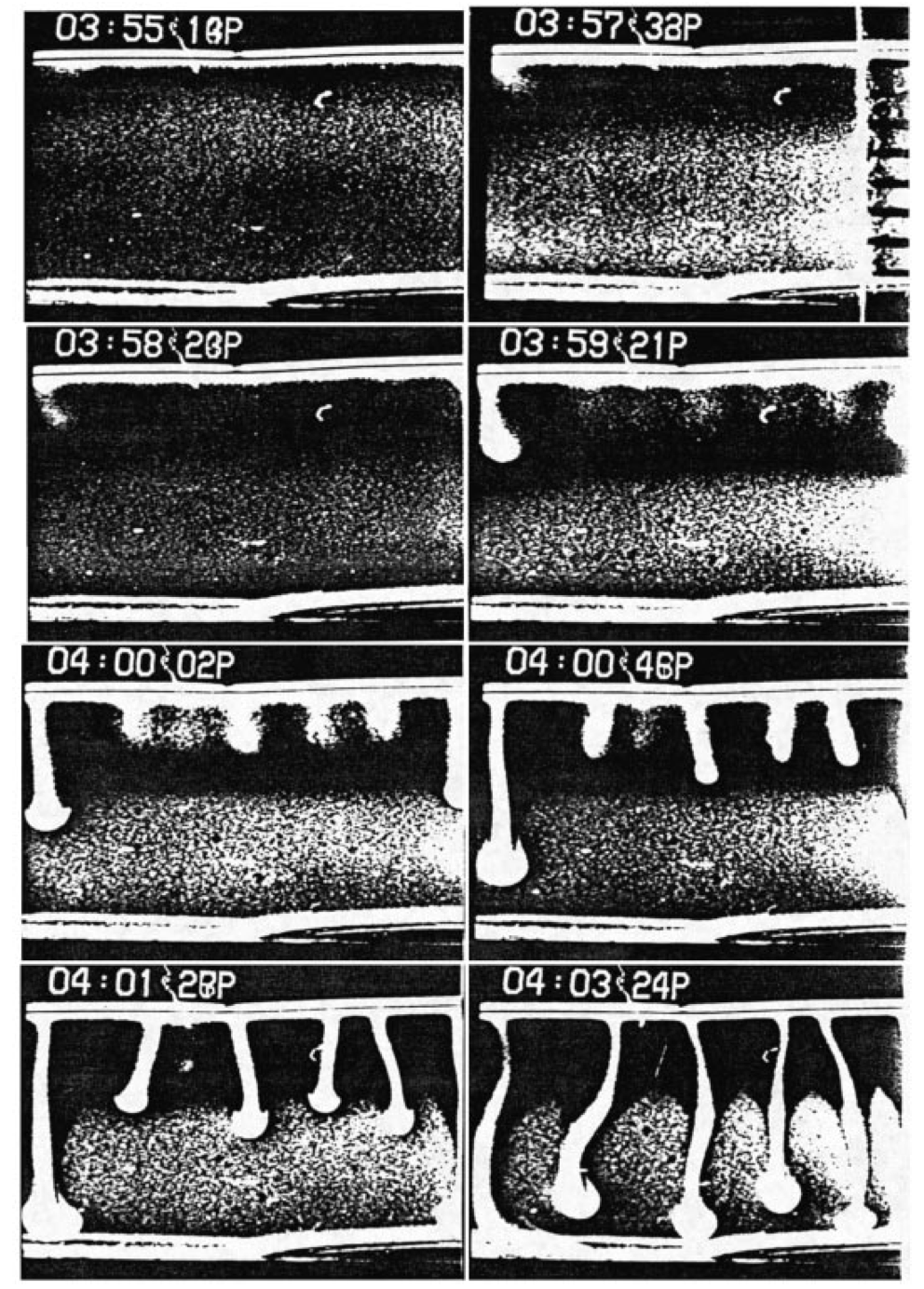
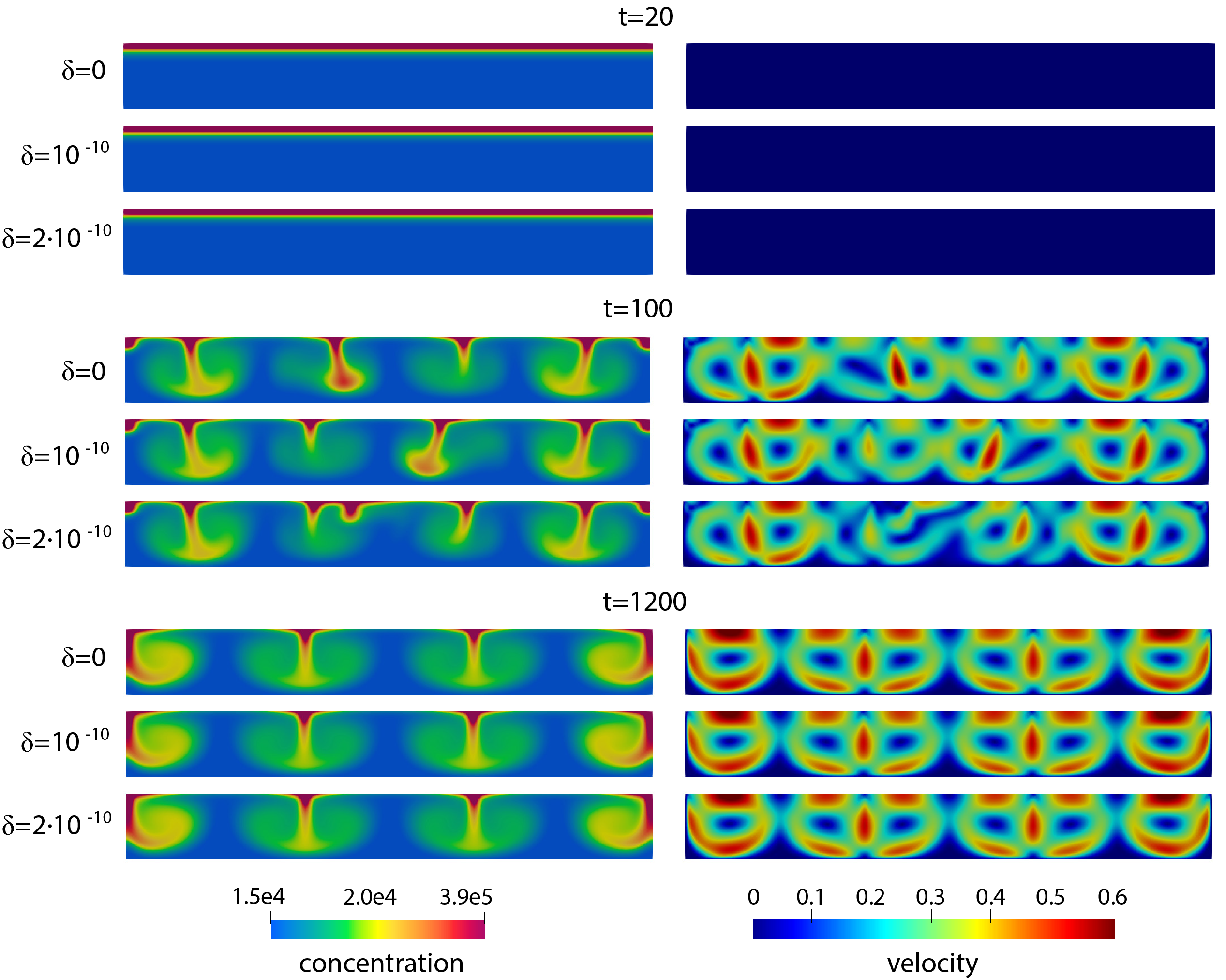
The system is modeled as the Navier-Stokes equations coupled with a convective transport equation, where fluid viscosity depends on cell concentration. The boundary conditions are modeled are Dirichlet for the fluid and Robin conditions for the concentration. The numerical scheme, inspired by Dr. Catalin Trenchea (U. Pitt) and Dr. Martina Bukač (U. Notre Dame), uses a second-order one-legged θ-Cauchy method in FreeFem++ (a finite element software in C++), decoupling the fluid and transport equations and solving them iteratively until convergence within a specified tolerance.
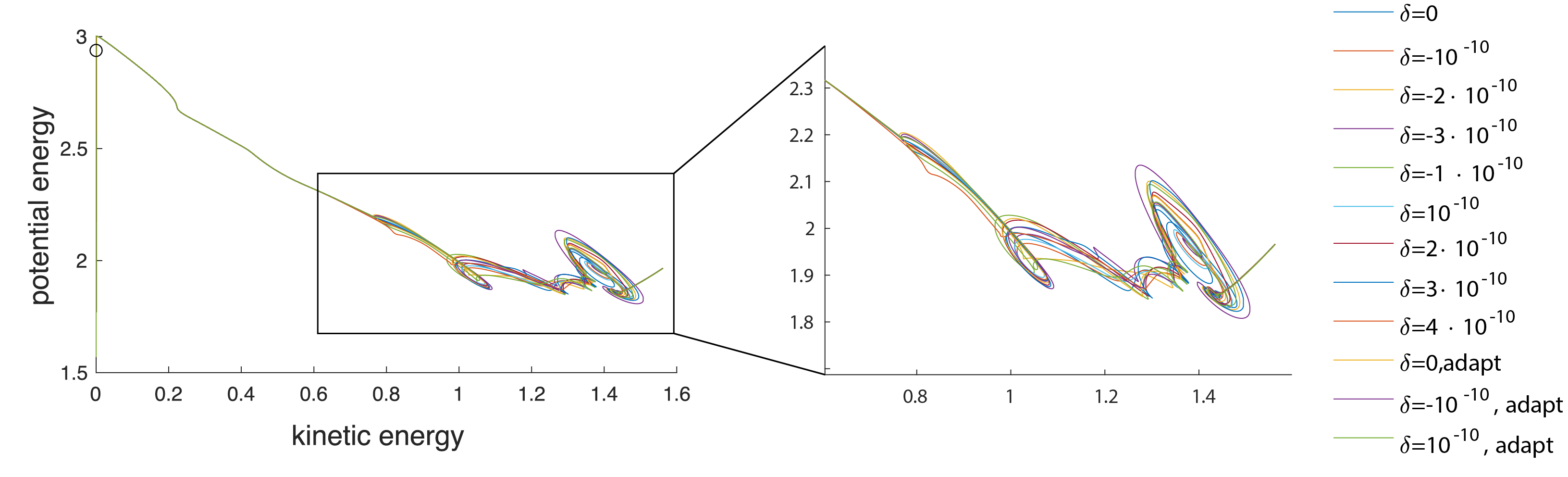
Small perturbations to the initial concentration reveal a regime where the system diverges into independent trajectories before converging to a stable state, indicating a chaotic-like region.
Future Extensions
Lorenz Applications to Bioconvection and PDE Analysis —
A closed-form solution to the system of equations would provide insight into the coupled eigenvalues of the fluid and concentration and allow analysis applied to a Lorenz system. Changes to the initial conditions and domain size provide ample opportunity for pattern analysis.
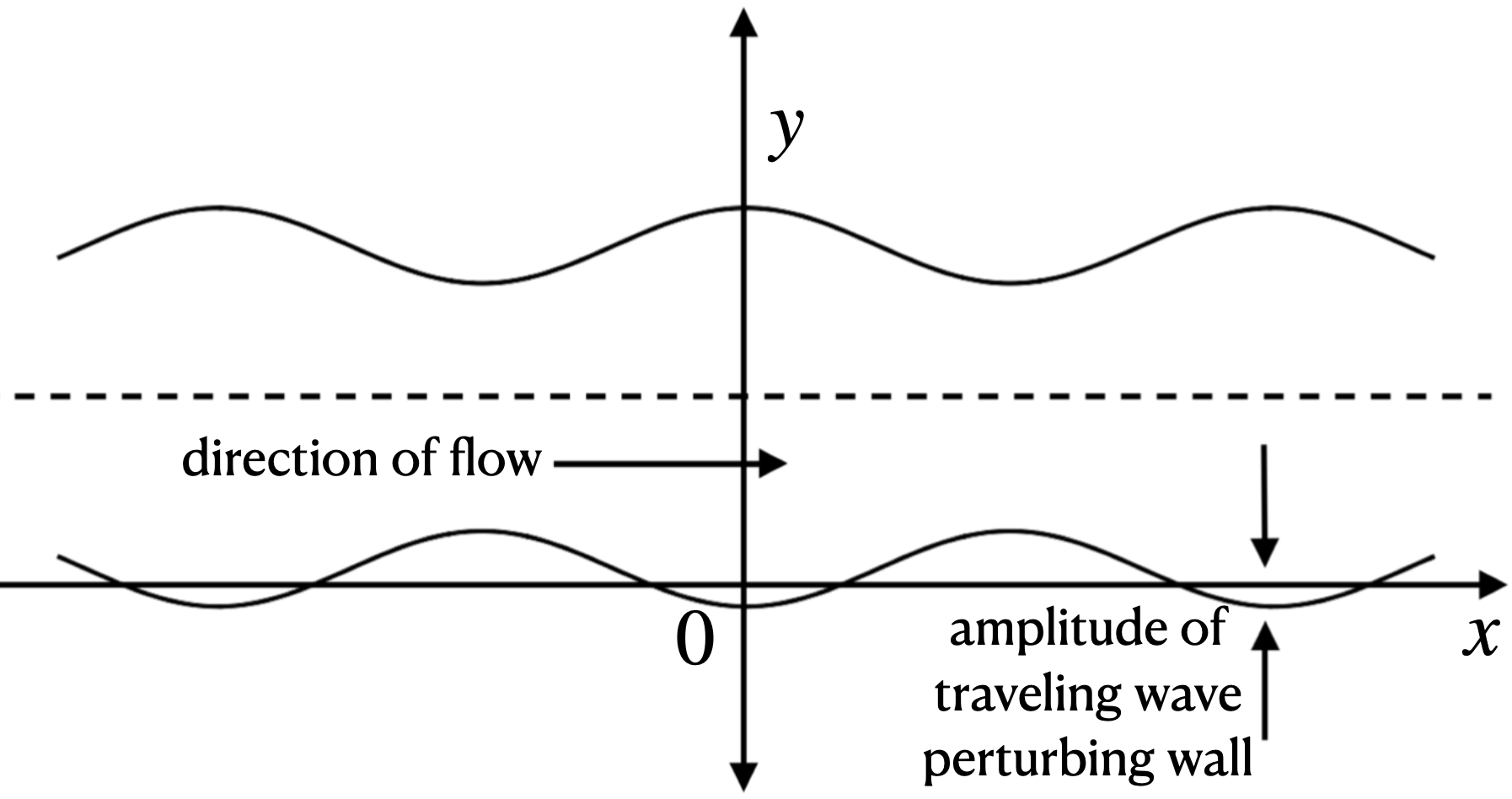
Blood Flow
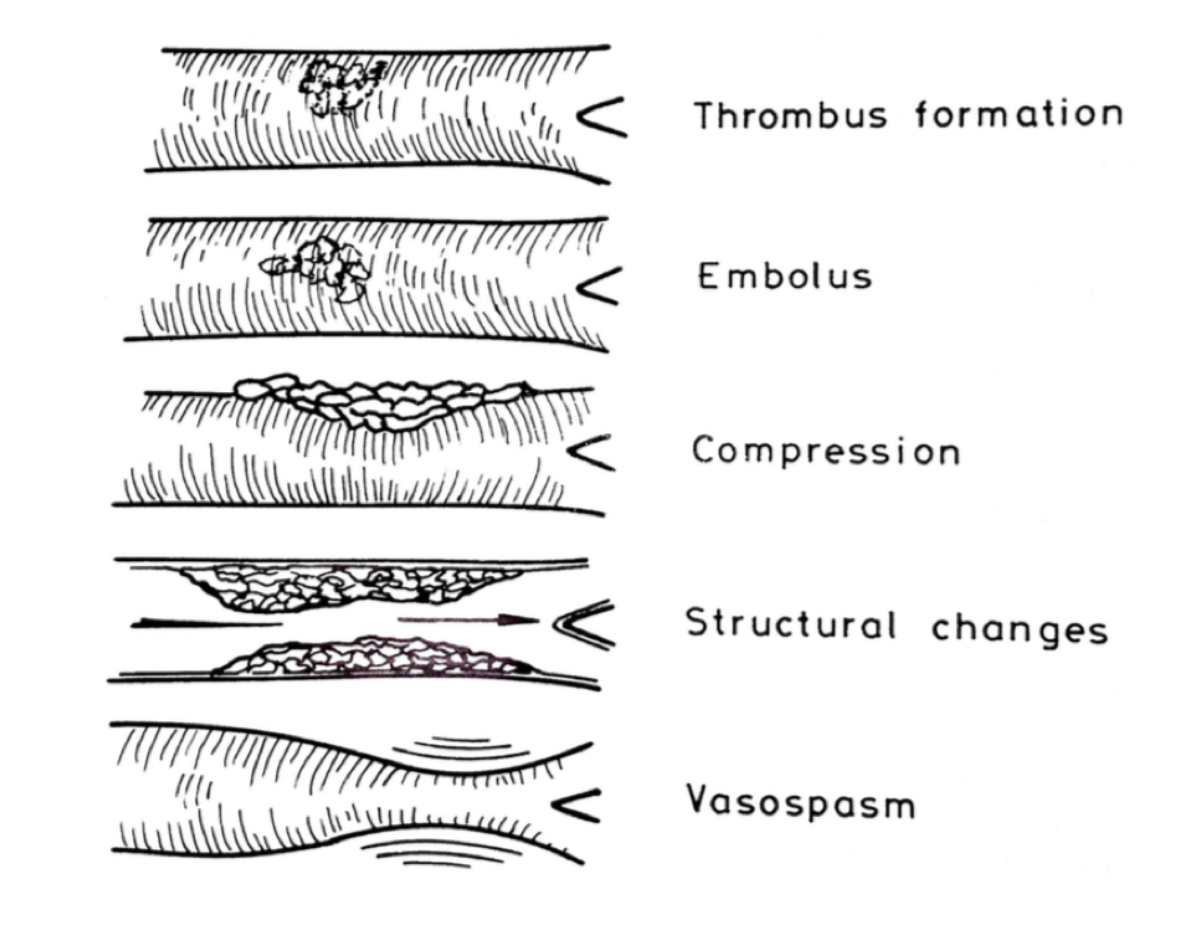
Flutter, a well-known phenomenon in fluid-structure interaction, occurs when the amplitude of a solid’s oscillation sharply increases due to energy transfer from fluid flow. Unlike resonance, which is driven by periodic forces at the natural frequency of a material, flutter results from self-excitation within the fluid-structure system. This instability can cause severe deformation and potential failure in structures such as aircraft wings, bridges, and even biological systems like blood vessels, although no analytical model for vascular flutter previously existed.
This work begins by defining the geometry of the channel and the properties of elastic, deformable walls. Wall distortion alters the fluid flow, changing the pressure distribution and, in turn, the channel shape. The system is defined as two PDEs with boundary conditions based on mass conservation and incompressibility. Linearizing the Navier-Stokes equations reduces the initial boundary value problem (IBVP) to an ODE using Fourier and Laplace transforms. The result provides a closed-form solution in the form of an infinite functional series.
Future Extensions
Extensions to 3D and Initial Conditions —
This work aims to extend the previous 2D closed form solution of blood flow into a 3D model. The initial phase involves first numerically validating the 2D analytical results to establish a foundation for more complex, biologically relevant models in three dimensions. This work aims to advance the field of biological flow modeling by providing deeper insights into the mathematical and computational aspects of blood flow dynamics in realistic settings.
Foreign Objects in Biological Fluid —
The influence of microplastics on blood flow is unknown. When considering their rigidity and resistance to decomposition this may lead to flow obstruction and vessel damage, negatively impacting one's immediate and longterm health. Three primary goals exist in this extension: (1) developing a baseline numerical model to incorporate microplastics as rigid bodies, (2) modeling fluid dynamics with microplastics using capillary slip conditions and rigid body interactions, examining particle accumulation and its implications for medical and industrial applications, and (3) exploring medical interventions to mitigate microplastic buildup, focusing on the filtration roles of the liver and kidneys. Using fluid-structure interaction models and stent optimization techniques, this research aims to propose strategies to counteract microplastic effects, providing novel insights into their impact on blood flow and contributing to biomedical modeling and public health.
Dynamical Systems and Neural Networks
State Modulation and Interneuron Subtypes
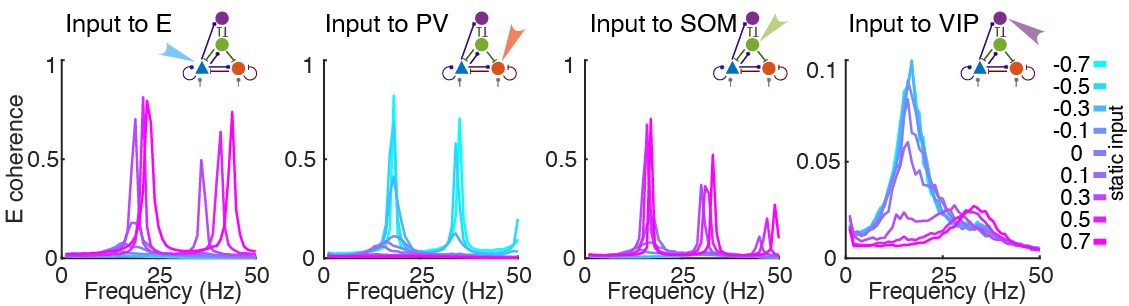
Our brains are made up of complex neural networks that help us navigate and modulate incoming stimulus from our environment. Neurons can be defined as excitatory and inhibitory, where excitatory neurons are responsible for the flow of synaptic information and inhibitory neurons help to regular that flow. Recent biological research has revealed many different types of inhibitory neurons while excitatory neurons display relatively homogeneous activity and morphologies. Therefore, this begs the question of the evolutionary advantage of the different types of inhibitory neurons and the role each distinct population plays in regulating brain activity.
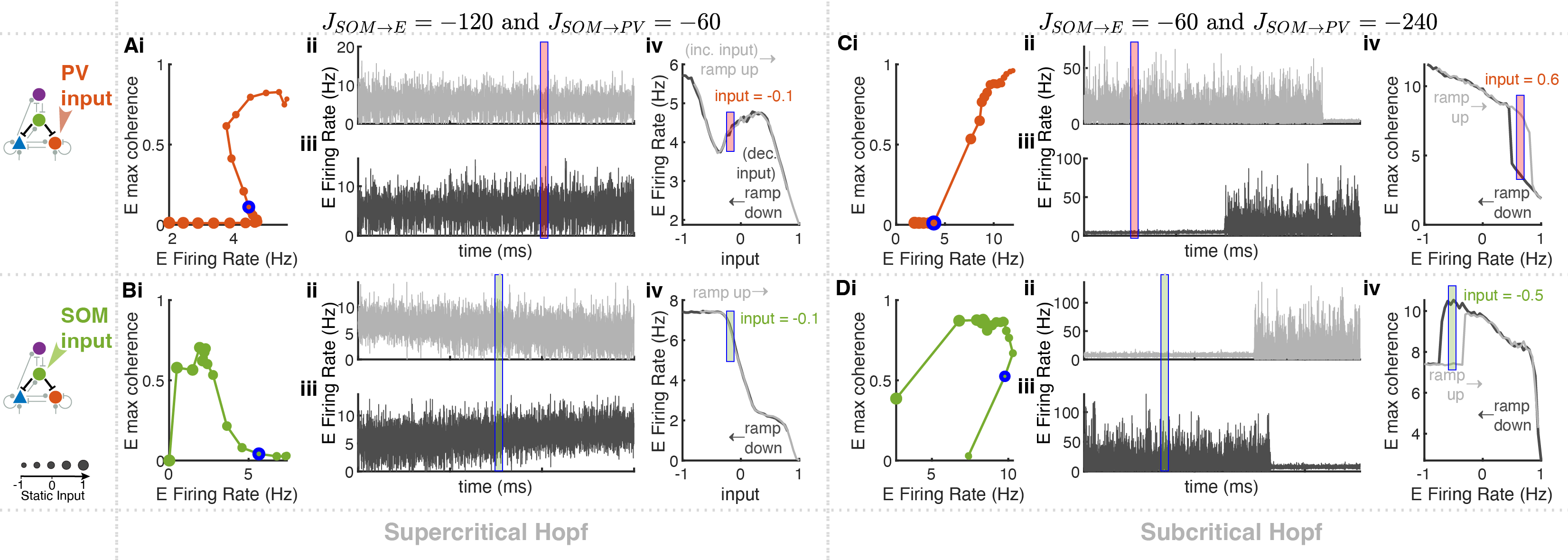
To this end, we design a four population interneuron network made up of excitatory (E) neurons and three inhibitory interneuron subtypes — parvalbumin (PV), somatostatin (SOM), and vasoactive intestinal peptide (VIP). Each neuron in the aforementioned population is modeled as an exponential integrate-and-fire (EIF) equation. Leveraging advancements in optogenetics (which allow cell-type-specific manipulations) and imbed biophysical relevant parameters and design in the computational model, we were able to probe the causal contributions of each interneuron subtype to circuit dynamics to understand the role of each population in the overall network response.
Future Extensions
Exploring Neural Network Dynamics through Mean Field Theory—
A promising direction for future research involves the use of ODEs and mean field theory to model neural network dynamics under various conditions. This project provides the opportunity to explore two-, three-, or four-population models, analyzing how alterations in single-cell properties or global network parameters influence overall network behavior.
Investigating the Statistical Characteristics of Neural Inputs—
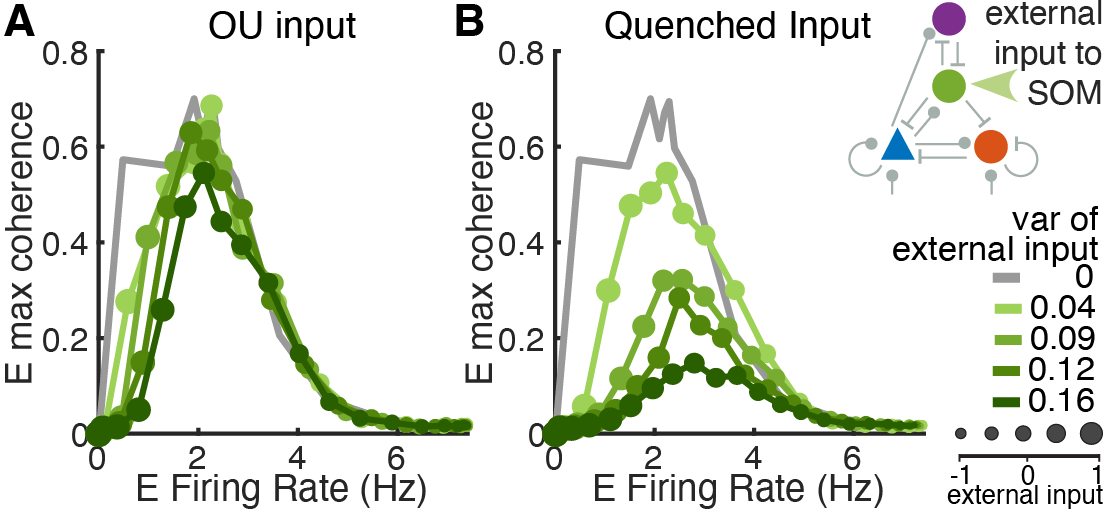
Another research avenue focuses on the statistical properties of neural network inputs and their impact on network dynamics. Utilizing methods such as principal component analysis (PCA), this extension aims to differentiate between first-order statistics (mean and variance) and second-order statistics (covariance and correlation) in various types of input noise, including static, quenched, and colored noise.
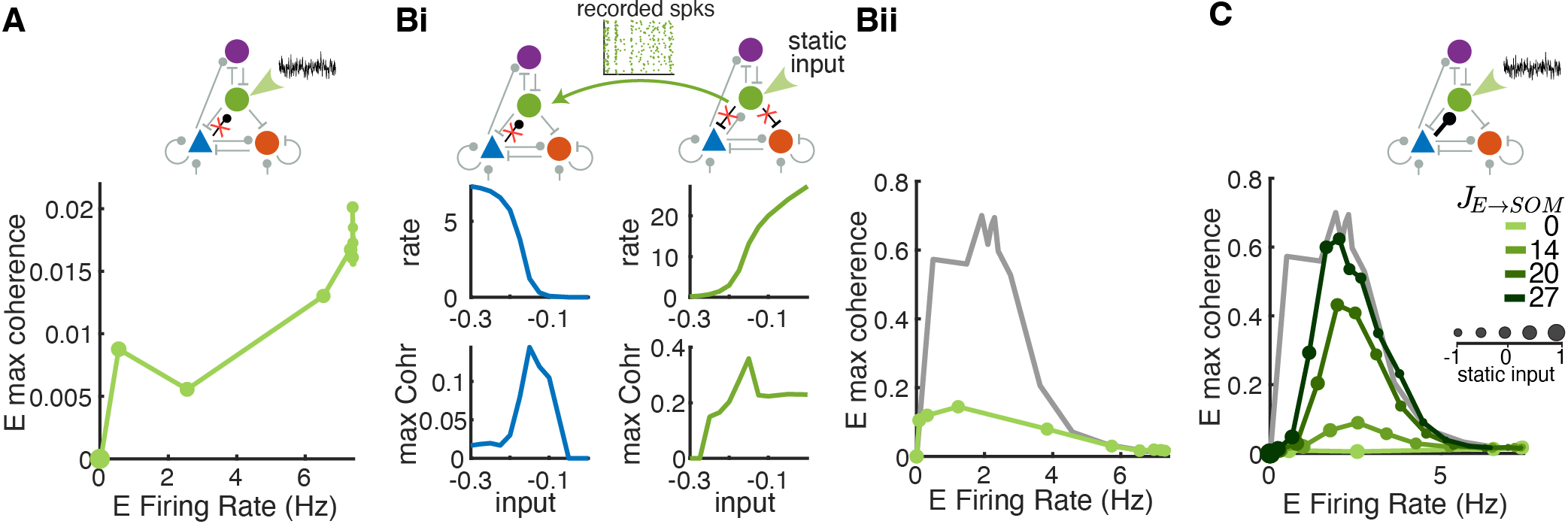
Modeling Neural Networks in Biological Contexts—
For those interested in connecting theoretical models with experimental data, this model is well suited to be manipulated to represent different brain regions and reflect experimental protocols or increasing the biophysical complexity and relevance of the model to advance research in mathematical biology and neuroscience.